Степень с действительным показателем с примерами решения

Оптимизация алгоритма [ править | править код ]

Как правило, операция возведения в квадрат выполняется быстрее операции умножения. Метод окон позволяет сократить количество операций умножения и, следовательно, сделать алгоритм возведения в степень более оптимальным .

Окно фактически представляет собой основание системы счисления . Пусть w — ширина окна, то есть за один раз учитывается w знаков показателя.

Рассмотрим метод окна.

1. Для i = 0 , 2 w − 1 ¯ <displaystyle i=<overline <0,2^-1>>>заранее вычисляется x i
2. Показатель степени представляется в следующем виде: n = ∑ i = 0 k / w n i ⋅ 2 i ⋅ w <displaystyle n=sum _^cdot 2^>>, где n i ∈ ( 0 , 1 , . . . , 2 w − 1 ) <displaystyle n_in <(0,1. 2^-1)>>
3. Пусть y — переменная, в которой будет вычислен конечный результат. Положим y = x n k / w <displaystyle y=x^>>.
4. Для всех i = k/w — 1, k/w — 2, …, 0 выполнить следующие действия:

1. y = y 2 w <displaystyle y=y^<2^>>
2. y = y ⋅ x n i <displaystyle y=ycdot x^>> .

В данном алгоритме требуется k возведений в квадрат, но число умножений в среднем сокращается до k/w .

Ещё более эффективным является метод скользящего окна. Он заключается в том, что ширина окна во время выполнения процесса может изменяться:

1. Показатель степени представляется в виде n = ∑ i = 0 l n i ⋅ 2 e i <displaystyle n=sum _^cdot 2^>>>, где n i ∈ ( 1 , 3 , 5 , . . . , 2 w − 1 ) <displaystyle n_in <(1,3,5. 2^-1)>>, а e_i+1 — e_i ≥ w.
2. Для i = ( 1 , 3 , 5 , . . . , 2 w − 1 ) <displaystyle i=(1,3,5. 2^-1)>вычисляется x i . Далее будем обозначать x i как x_i.
3. Пусть y — переменная, в которой будет вычислен конечный результат. Положим y = x n l <displaystyle y=x^>>.
4. Для всех i = l — 1, l — 2, …, 0 выполнить следующие действия:

1. Для всех j от 0 до e_i+1 — e_i — 1 y возвести в квадрат
2. j = m i <displaystyle j=m_>
3. y = y ⋅ x j <displaystyle y=ycdot x_>

Для всех j от 0 до e — 1 y возвести в квадрат .

Количество операций возведения в степень в данном алгоритме такое же, как и в методе окна, а вот количество операций умножений сократилось до l, то есть до k w + 1 <displaystyle <frac >> в среднем .

Для примера возведём методом скользящего окна число x в степень 215. Ширина окна w = 3.

1. 215 = 2 7 + 5 · 2 4 + 7
2. y = 1
3. y = y · x = x
4. y 3 раза возводится в квадрат, так как на данном шаге e₂ — e₁ −1 = 7 — 4 — 1 = 2, а отсчёт ведётся с нуля, то есть y = y 8 = x 8
5. y = y · x 5 = x 13
6. y 4 раза возводится в квадрат, так как на данном шаге e₁ — e −1 = 4 — 0 — 1 = 3, то есть y = y 16 = x 208
7. y = y · x 7 = x 215

«Надстрочный знак» в Word, чтобы напечатать любую степень числа

Как на клавиатуре написать верхнюю запятую

В Word есть встроенная кнопка, при помощи которой можно написать степень числа на клавиатуре. Она называется «Надстрочный знак» («X²») и располагается во вкладке «Главная».

Рис. 2 (Клик для увеличения). «Надстрочный знак» («X²») во вкладке «Главная» позволяет написать степень числа.

1. Сначала следует напечатать число, которому необходимо придать вид степени.
2. Затем выделить его.
3. И в заключение нажать на «X²» (рис. 2).

Кроме цифр, можно также превращать в степень и буквы. Так можно сделать текст маленького размера и поместить его наверху строки текста.

Такое выделение текста, возможно, кому-то понадобится в разных ситуациях. Так что кнопка Ворда для написания степени числа является универсальной. Она превращает в «степень» любую последовательность символов.

Выделение устойчивого выражения

В предыдущих примерах мы преобразовывали разные виды показательных уравнений путем разложения многочленов на множители, потому что хотели найти способ решения — получить одинаковые основания или выделить переменную, которую можно заменить. Так вот, когда мы выносим некий множитель за скобку или заменяем переменную, пытаясь упростить уравнение — это действие по сути и является выделением устойчивого выражения.

Устойчивое выражение — это некий многочлен, содержащий переменную, который в скрытом виде присутствует во всех показательных функциях уравнения. Его можно вынести за скобки или обозначить новой переменной, чтобы упростить уравнение.

Хорошая новость: так или иначе устойчивое выражение можно найти почти в любом трудном уравнении. Проблема только в том, чтобы научиться верно определять такое выражение, а этот навык появляется лишь с опытом.

Пример 1

3х+1 + 3х — 3х-2 = 35

В данном случае в качестве устойчивого выражения удобно взять 3х-2 как степень с наименьшим показателем. В итоге мы получим:

3х-2(33 + 32 — 1) = 35

3х-2 × 35 = 35

3х-2 = 1

Поскольку 1 равняется любое число в нулевой степени, мы можем записать:

3х-2 = 3

х — 2 = 0

х = 2

Пример 2

5 × 3-3х+1 + 3-3х+2 = 24

Для начала мы попробуем в левой части уравнения получить одинаковую степень: 3-3х+2 = 3-3х+1+1 = 3 × 3-3х+1.

Теперь у нас есть устойчивое выражение 3-3х+1, которое можно вынести за скобки, чтобы получить более простое уравнение:

3-3х+1(5+3) = 24

8 × 3-3х+1 = 24

3-3х+1 = 31

-3х + 1 = 1

х = 0

Приведение к одинаковой степени

Не все показательные уравнения с разными основаниями можно решить предыдущим способом. Иногда проще преобразовать не основания, а показатели степени. Правда, пользоваться этим методом есть смысл только в том случае, когда мы имеем дело с умножением или делением.

При умножении чисел с разными основаниями, но одинаковыми степенными показателями можно перемножить только основания (степень останется прежней): axbx = (ab)x.

Пример

52х-4 = 492-х

Общих множителей у левой и правой части уравнения нет и привести их к одинаковому основанию достаточно трудно. Поэтому стоит поработать с показателями степеней:

52х-4 = 492-х

52х-4 = 74-2х

52х-4 = (1/7)2х-4

352х-4 = 1

2х — 4 = 0

х = 2

Пример 2

2х-2 = 52-х

Нам нужно привести обе части уравнения к одинаковым степенным показателям, и для этого вначале попробуем преобразовать правую часть, используя свойство степенных функций.

2х-2 = 1/5х-2

Теперь умножим обе части на 52-х и придем к уравнению:

2х-2 × 52-х = 1

10х-2 = 1

10х-2 = 10

х — 2 = 0

х = 2

Пишем степень на клавиатуре

Вначале рассмотрим два универсальных метода, первый из которых можно использовать везде, а второй в большинстве случаев.

Первый. Для указания степени вы можете использовать специальный символ «^» (комбинация клавиш Shift + 6 в раскладке транслита). Используется примерно так. Если вам, к примеру, нужно записать 10 в 20-й степени, то пишите 10 ^ 20. Стоит отметить, что такая запись считается практически универсальной, так как этот символ есть в любой кодировке и не требует каких-то хитростей.

Второй. Это использование специальных символов, которые можно записывать с помощью кнопки Alt и цифр в правой колодке клавиш клавиатуры (для ее включения нужно нажать клавишу NumLock, после этого обязательно проверьте, что на клавиатуре загорелась соответствующая лампочка). Однако, есть ограничение. Поддерживаются всего две степени — это возведение в квадрат и в куб. Для 2-й степени используется комбинация Alt + 0178 (зажимаете Alt, набираете код из цифр, а затем отпускаете Alt), а для 3-й степени используется комбинация клавиш Alt + 0179. Эти символы поддерживаются практически во всех редакторах текстов и документов.

Примечание: Учтите, что в ноутбуках колодка клавиш с цифрами может включаться с помощью клавиши Fn (в зависимости от модели, могут быть разные комбинации).

Примечание: Кстати, вы так же можете использовать таблицу символов, как это было продемонстрировано в обзоре для символа корня.

Производная показательной функции

Вычислим среднюю скорость роста показательной функции у= на отрезке :

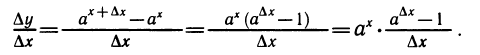
Мы видим, что средняя скорость роста показательной функции на отрезке равна значению этой функции в точке х, умноженному на число. Исследуем, как ведет себя это число при маленьких значениях ∆х. Так как а°=1, то значение при маленьких значениях ∆х близко к 1. Если на графике функции проведем секущую, проходящую через точки (0; 1) и ( ∆х; ), то ее угловой коэффициент будет равен числу =tg a (рис. 106).

При секущая будет приближаться к касательной к

графику функции в точке (0; 1). Это означает, что будет

приближаться к произведению на значение производной при х=0. Итак, для нахождения производной функции у= надо знать только значение этой производной в нуле. Если мы его обозначим через k, то получим формулу

т. е. производная показательной функции пропорциональна самой функции.

Как же найти коэффициент пропорциональности k? Мы знаем, что он равен угловому коэффициенту касательной, проведенной в точке (0; 1). Можно приближенно по графику вычислить этот коэффициент. Так, известно, что для а=10 значение k ≈2,3, поэтому

С помощью знака предела коэффициент k можно записать так:

3. Число е

Посмотрим на графики показательных функций при различных а (рис. 105). Все они проходят через точку М (0; 1). Проведем в этой точке касательные к графикам. Мы видим, что, чем больше основание а, тем «круче» касательная. Так, при а = 2 угловой коэффициент касательной равен 0,693, а при а=10 угловой коэффициент касательной равен 2,303. Ясно, что при непрерывном изменении а от 2 до 10 угловой коэффициент касательной в точке М будет непрерывно меняться и найдется такое значение а, для которого этот коэффициент будет равен единице. Такое основание а обозначается буквой е. Число е иррационально. Его приближенное значение таково: е ≈ 2,718.

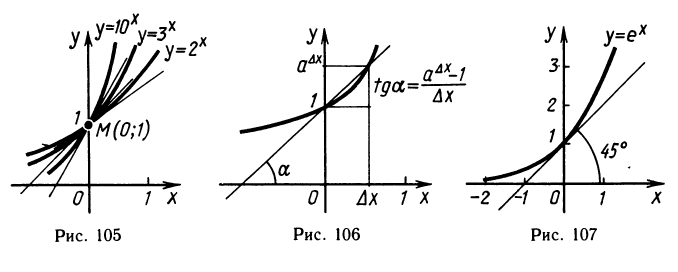
Итак, е — это такое число, что угловой коэффициент касательной к графику функции у=в точке х = 0 равен единице, т. е. касательная в этой точке образует с осью абсцисс угол 45° (рис. 107).

Можно сказать иначе. Мы уже знаем, что производная любой показательной функции пропорциональна самой этой функции. Число е — это основание, для которого коэффициент пропорциональности равен единице, т. е. е — это такое число, что производная функции у = равна самой этой функции:

Функцию у = часто обозначают у = ехр х (читается: «Эксп от х») и называют экспонентой. Экспонентами называют и функции более общего вида: у = . Подумайте, понятен ли вам смысл таких распространенных выражений: «Численность бактерий растет по экспоненте», «Сила тока затухает по экспоненте», «Его успехи растут по экспоненте».

Как печатать знаки ударения над буквами в Microsoft Word

Если у вас нет специальной клавиатуры, вам придётся делать немного дополнительных действий, чтобы набирать буквы с ударением в Microsoft Word. Вот несколько способов сделать это. Если вы печатаете регулярно на другом языке, кроме английского, у вас, вероятно, уже все получилось. Возможно, вы даже используете специализированную клавиатуру, которая упрощает ввод букв с акцентом. Но если вы печатаете в основном на английском или русском языке, иногда вам может понадобиться набрать букву со знаком акцента. В конце концов, английский использует много слов, заимствованных из других языков, таких как, например, дежавю, халапеньо, доппельгангер и резюме. И хотя мы, как правило, просто вводим эти слова без акцента на английском языке, иногда приятно использовать более формальный подход. В тех случаях, когда вы это делаете, Microsoft Word предоставляет несколько простых способов сделать это.

Степени с рациональными показателями

Степени с действительными показателями. Будем, как и в п. 11, рассматривать только корни из положительных чисел. Мы видели, что в случае, когда m делится нацело на n,

Обобщая это правило, можно ввести следующее определение степени с положительным рациональным показателем p/q:

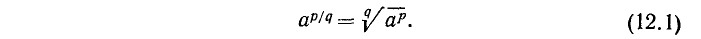
В случае отрицательного рационального показателя степени —p/q полагают (по аналогии со случаем целого отрицательного показателя степени)

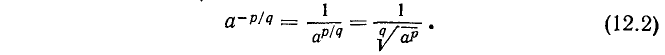
На степени с рациональными показателями распространяются все правила действий над степенями с натуральными и вообще целыми показателями. Для их обоснования достаточно применить правила п. 11 действий над корнями. Докажем, например, свойство

Имеем

Так же получим Отсюда

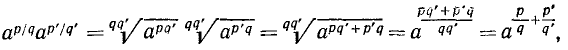
что и требовалось доказать.

Рассматривают также степени положительного числа а при произвольных действительных показателях. В основу определения при иррациональном х кладется последовательное приближение х рациональными числами. Так, например, для следует рассмотреть приближения по недостатку и по избытку для и возводить 3 в соответствующие рациональные степени, записывая

По мере продолжения этого процесса левая и правая части неравенств, выраженные бесконечными десятичными дробями, будут иметь все большее и большее число совпадающих десятичных знаков, которые и будут приниматься за десятичные знаки, определяющие иррациональное число . Более подробно рассматривать этот вопрос мы не можем, но отметим, что имеет действительное вполне определенное значение при а > 0 и любом действительном х.

Замечание:

Извлечение корня нечетной степени возможно и из отрицательного числа. Поэтому выражению при а < 0 также можно приписать смысл с помощью равенства в случае, когда несократимая рациональная дробь p/q имеет нечетный знаменатель. В случае четного q и для иррациональных значений показателя степень отрицательного основания не определяется. Нуль в любой положительной степени равен нулю; нулевая и отрицательные степени нуля не определены.

Пример:

Произвести действия, пользуясь отрицательными и дробными показателями степени: .

Решение:

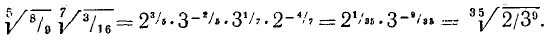
Аксиоматическое определение показательной функции

Показательная функция y = f(x), где f(x) = , обладает замечательным свойством:

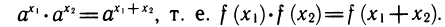
Это свойство может быть положено в основу определения показательной функции.

Пусть функция f задана на всей числовой оси R и для любых чисел x₁,x₂ удовлетворяет соотношению

Написанное соотношение называют функциональным уравнением. Вопрос можно поставить так: каковы функции f с областью определения R, удовлетворяющие функциональному уравнению

Прежде всего функция f {х) = 0 удовлетворяет этому уравнению. Будем считать, что f не является тождественным нулем. Из функционального уравнения следует цепочка свойств функции /, которые мы перечислим в виде серии нетрудных задач с указаниями на то, как их надо решать.

1)f(0)=1 (рассмотреть f(x+O), где х — какое-либо число, для которого f(x) ≠ 0).

2) f(х) ≠ 0 для любого х (рассмотреть f (x + ( — x))).

3) f(x)>0 для любых х (рассмотреть )

4) (рассмотреть f (x + ( —x))).

Обозначим f(1) через а.

5) где n ∈ N (рассмотреть f (1 + 1+ …-+-1)).

6) , где n ∈ N (воспользоваться 4) и 5)).

7) где n ∈ N (рассмотреть .

8) f(r) = ar, где r — рациональное число.

Таким образом, мы видим, что значения всякой, не равной тождественно нулю функции, определенной на всей числовой оси и удовлетворяющей функциональному уравнению f( x₁)-f( x₂) = f(x₁+x₂), для рациональных значений аргумента г совпадают со значениями а’ при некотором а. Для того чтобы сделать вывод о том, что f (х) совпадает с при любом вещественном х, одного функционального уравнения мало. Надо добавить еще какое-либо свойство — монотонность или непрерывность. Вот почему, стараясь избежать трудоемкого описания значений показательной функции с помощью рациональных приближений, часто дают следующее определение показательной функции:

Показательная функция y = f (х) — это строго монотонная функция, определенная на всей числовой оси и удовлетворяющая функциональному уравнению

В одном мгновеньи видеть вечность, Огромный мир — в зерне песка, В единой горсти — бесконечность И небо — в чашечке цветка.

У. Блейк, пер. С. Маршака

Приоритет операций:

Для указания (или изменения) приоритета операций необходимо использовать скобки (), например: (a+b)/4 — тут вначале будет произведено сложение a+b, а потом сумма разделится на 4, тогда как без скобок: — сначала b разделится на 4 и к полученному прибавится a

ВНИМАНИЕ! В непонятных случаях лучше всегда использовать скобки для получения нужного результата, например: 2^4^3 — неясно как будет вычислено это выражение: cначала 2^4, а затем результат в степень 3, или сначала 4^3=64, а затем 2^64? Поэтому, в данном случае, необходимо использовать скобки: (2^4)^3 или 2^(4^3) — смотря что нужно. Также распространенной ошибкой является запись вида: x^3/4 — непонятно: вы хотите возвести x в куб и полученное выражение разделить на 4, или хотите возвести x в степень 3/4? В последнем случае необходимо использовать скобки: x^(3/4)

Степень с натуральным показателем, квадрат числа, куб числа

Для начала дадим определение степени числа с натуральным показателем. Забегая вперед, скажем, что определение степени числа a с натуральным показателем n дается для действительного числа a, которое будем называть основанием степени, и натурального числа n, которое будем называть показателем степени. Также отметим, что степень с натуральным показателем определяется через произведение, так что для понимания нижеизложенного материала нужно иметь представление об умножении чисел.

Из данного определения понятно, что с помощью степени с натуральным показателем можно кратко записывать произведения нескольких одинаковых множителей. Например, 8·8·8·8 можно записать как степень 84. Это аналогично тому, как с помощью произведения записывается сумма одинаковых слагаемых, к примеру, 8+8+8+8=8·4 (смотрите статью общее представление об умножении натуральных чисел).

Сразу стоит сказать о правилах чтения степеней. Универсальный способ чтения записи an таков: «a в степени n». В некоторых случаях также допустимы такие варианты: «a в n-ой степени» и «n-ая степень числа a». Для примера возьмем степень 812, это «восемь в степени двенадцать», или «восемь в двенадцатой степени», или «двенадцатая степень восьми».

Вторая степень числа, а также третья степень числа имеют свои названия. Вторую степень числа называют квадратом числа, например, 72 читается как «семь в квадрате» или «квадрат числа семь». Третья степень числа называется кубом числа, к примеру, 53 можно прочитать как «пять в кубе» или сказать «куб числа 5».

Пришло время привести примеры степеней с натуральными показателями. Начнем со степени 57, здесь 5 – основание степени, а 7 – показатель степени. Приведем еще пример: десятичная дробь 4,32 является основанием, а натуральное число 9 – показателем степени (4,32)9.

Обратите внимание, что в последнем примере основание степени 4,32 записано в скобках: чтобы избежать разночтений мы будем брать в скобки все основания степени, которые отличны от натуральных чисел. В качестве примера приведем следующие степени с натуральными показателями , их основания не являются натуральными числами, поэтому они записаны в скобках

Ну и для полной ясности в этом моменте покажем разницу, заключенную в записях вида (−2)3 и −23. Выражение (−2)3 – это степень отрицательного числа −2 с натуральным показателем 3, а выражение −23 (его можно записать как −(23)) соответствует числу, противоположному значению степени 23.

Заметим, что встречается обозначение степени числа a с показателем n вида a^n. При этом, если n – многозначное натуральное число, то показатель степени берется в скобки. Например, 4^9 – это другая запись степени 49. А вот еще примеры записи степеней при помощи символа «^»: 14^(21), (−2,1)^(155). В дальнейшем мы преимущественно будем пользоваться обозначением степени вида an.

Данное выше определение позволяет находить значение степени с натуральным показателем. Для этого нужно вычислить произведение n одинаковых множителей, равных a. Эта тема заслуживает детального рассмотрения в отдельной статье – смотрите возведение в степень с натуральным показателем.

Одной из задач, обратной возведению в степень с натуральным показателем, является задача нахождения основания степени по известному значению степени и известному показателю. Эта задача приводит к понятию корня из числа.

Также стоит изучить свойства степени с натуральным показателем, которые вытекают из данного определения степени и свойств умножения.

Примеры решения задач [ править | править код ]

Применяя алгоритм, вычислим 21 13 :

13 10 = 1101 2 <displaystyle 13_<10>=1101_<2>> m 3 = 1 , m 2 = 1 , m 1 = 0 , m 0 = 1 <displaystyle m_<3>=1,m_<2>=1,m_<1>=0,m_<0>=1> 21 13 = ( ( ( 1 ⋅ 21 m 3 ) 2 ⋅ 21 m 2 ) 2 ⋅ 21 m 1 ) 2 ⋅ 21 m 0 = ( ( ( 1 ⋅ 21 1 ) 2 ⋅ 21 1 ) 2 ⋅ 21 0 ) 2 ⋅ 21 1 = ( ( ( 1 ⋅ 21 ) 2 ⋅ 21 ) 2 ⋅ 1 ) 2 ⋅ 21 = ( ( 21 2 ⋅ 21 ) 2 ) 2 ⋅ 21 = ( ( 441 ⋅ 21 ) 2 ) 2 ⋅ 21 = 85766121 2 ⋅ 21 = 154472377739119461 <displaystyle <egin21^<13>&=(((1cdot 21^>)^<2>cdot 21^>)^<2>cdot 21^>)^<2>cdot 21^>\&=(((1cdot 21^<1>)^<2>cdot 21^<1>)^<2>cdot 21^<0>)^<2>cdot 21^<1>\&=(((1cdot 21)^<2>cdot 21)^<2>cdot 1)^<2>cdot 21\&=((21^<2>cdot 21)^<2>)^<2>cdot 21\&=((441cdot 21)^<2>)^<2>cdot 21\&=85766121^<2>cdot 21\&=154472377739119461end0>1>2>3>>>

Вставить ударенные буквы с помощью сочетаний клавиш

В Word много отличных сочетаний клавиш, и сочетания клавиш с акцентированными символами не являются исключением. Вы, возможно, уже заметили на экране «Больше символов», что Word подсказывает нам, что это за комбинация клавиш для этого символа.

И самое приятное то, что эти ярлыки следуют своего рода формуле, поэтому вам не обязательно запоминать их все. Вы будете использовать клавишу Ctrl или Shift вместе с клавишей акцента на клавиатуре, после чего следует быстрое нажатие буквы.

Например, чтобы получить символ, вы должны нажать Ctrl + э (’ — апостроф на английской раскладке), отпустить эти клавиши, а затем быстро нажать клавишу a.

Обратите внимание, что если вы хотите использовать Á вместо á, вам нужно включить блокировку заглавных букв, прежде чем использовать клавишу быстрого доступа, так как использование клавиши Shift изменит сочетание клавиш. Переключение регистра букв с ударением делается следующим образом: нажмите одновременно CTRL+SHIFT+буква и затем отпустите их перед тем, как печатать букву с ударением

Это переключит регистр буквы — повторите ещё раз, чтобы вновь переключить регистр с заглавного на прописной или наоборот.

Следующая таблица показывает популярные сочетания клавиш для вставки знаков акцента и ударения. В этих сочетаниях нужно одновременно нажимать две или более клавиш. Клавиши, которые нужно нажать одновременно, соединены знаком плюс (+), а клавиши, которые нужно нажать сразу после другой клавиши, соединены запятой (,).

Что представляют собой степенные выражения

an,

здесь а представляет собой основание степени, n определяет ее показатель.

Таким образом, можно составить формулу:

an=a×a×a…×a

Запись можно прочитать, как «a в степени n».

Перед тем, как рассмотреть действия со степенными выражениями, полезно вспомнить свойства степени:

1. Произведение степеней. Если степени, которые требуется умножить, имеют одинаковые основания, то основание оставляют неизменным, а показатели степеней суммируют. То есть, an×am=am+n, где а является основанием степени, n и m — это показатели степени в виде каких-либо натуральных чисел.
2. Частное степеней. При делении степеней, имеющих одинаковые основания, следует оставить основание прежним, а показатель степени делимого уменьшить на показатель степени делителя. Например, aman=am-n, где а является основанием степени, n и m — это показатели степени в виде каких-либо натуральных чисел, m>n.
3. Возведение степени в квадрат. При возведении степени в степень основание степени сохраняют прежним, а показатели перемножают. К примеру, (an)m=an×m, где а является основанием степени, n и m — это показатели степени в виде каких-либо натуральных чисел.
4. Степень произведения. Для того чтобы возвести в степень произведение, требуется каждый из множителей возвести в эту степень. Результаты, которые получились в итоге, необходимо перемножить. То есть: (a×b)n=an×bn, где а и b являются основаниями степени, n — это показатель степени в виде какого-либо натурального числа.
5. Степень частного. Для возведения в степень частного нужно возвести в данную степень по отдельности делимое и делитель. Затем первый получившийся результат следует разделить на второй. К примеру, (a÷b)n=an÷bn, где а и b являются основаниями степени, не равными нулю, n — это показатель степени в виде какого-либо натурального числа.

Как пользоваться таблицей степеней числа два?

Первый столбец — это степень двойки, который одновременно, обозначает число бит, которое представляет число.

Второй столбец — значение двойки в соответствующей степени (n). 

Пример нахождения степени числа 2. Находим в первом столбце число 7. Смотрим по строке вправо и находим значение два в седьмой степени (27) — это 128

Третий столбец — максимальное число, которое можно представить с помощью заданного числа бит (в первом столбце). 

Пример определения максимального целого числа без знака. Если использовать данные из предыдущего примера, мы знаем, что 27 = 128. Это верно, если мы хотим понять, какое количество чисел, можно представить с помощью семи бит. Но, поскольку первое число — это ноль, то максимальное число, которое можно представить с помощью семи бит 128 — 1 = 127 . Это и есть значение третьего столбца.

Степень двойки (n)	Значение степени двойки 2n	Максимальное число без знака, записанное с помощью n бит	Максимальное число со знаком,  записанное с помощью n бит
1	—	—
1	2	1	—
2	4	3	1
3	8	7	3
4	16	15	7
5	32	31	15
6	64	63	31
7	128	127	63
8	256	255	127
9	512	511	255
10	1 024	1 023	511
11	2 048	2 047	1023
12	40 96	4 095	2047
13	8 192	8 191	4095
14	16 384	16 383	8191
15	32 768	32 767	16383
16	65 536	65 535	32767
17	131 072	131 071	65 535
18	262 144	262 143	131 071
19	524 288	524 287	262 143
20	1 048 576	1 048 575	524 287
21	2 097 152	2 097 151	1 048 575
22	4 194 304	4 194 303	2 097 151
23	8 388 608	8 388 607	4 194 303
24	16 777 216	16 777 215	8 388 607
25	33 554 432	33 554 431	16 777 215
26	67 108 864	67 108 863	33 554 431
27	134 217 728	134 217 727	67 108 863
28	268 435 456	268 435 455	134 217 727
29	536 870 912	536 870 911	268 435 455
30	1 073 741 824	1 073 741 823	536 870 911
31	2 147 483 648	2 147 483 647	1 073 741 823
32	4 294 967 296	4 294 967 295	2 147 483 647

Необходимо принять во внимание, что не все числа в компьютере представлены таким образом. Существуют и другие способы представления данных

Например, если мы хотим записывать не только положительные, но и отрицательные числа, то нам потребуется еще один бит для хранения значения «плюс/минус». Таким образом, количество бит, предназначенных для хранения чисел у нас уменьшилось на один. Какое максимальное число может быть записано в виде целого числа со знаком можно посмотреть в четвертом столбце.

Для этого же самого примера ( 27) семью битами можно записать максимум число +63, поскольку один бит занят знаком «плюс». Но мы можем хранить и число «-63», что было бы невозможно, если бы все биты были бы зарезервированы под хранение числа.

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым
числом — положительным, отрицательным или нулём.

Запомните!

При возведении в степень положительного числа
получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться
как положительное число, так и отрицательное число. Это зависит от того чётным или
нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень,
то получается отрицательное число. Так как произведение
нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число.
Так как произведение чётного количество отрицательных сомножителей положительно.

Запомните!

Отрицательное число, возведённое в
чётную степень, есть число
положительное.

Отрицательное число, возведённое в
нечётную степень, — число
отрицательное.

Квадрат любого числа есть положительное число или нуль, то есть: при любом .

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи
и
это разные выражения. Результаты возведения
в степень данных выражений будут разные.

Вычислить означает найти значение четвёртой степени отрицательного числа.

В то время как найти «» означает, что пример нужно решать в 2 действия:

1. Возвести в четвёртую степень положительное число .
2. Поставить перед полученным результатом знак «минус» (то есть выполнить
   действие вычитание).

Пример. Вычислить:

Использование Alt-кодов

Установите курсор сразу за цифрой, для которой желаете указать степень. Затем включите цифровую клавиатуру, что находится справа от основной клавиатуры, с помощью кнопки Num Lock.

Теперь нажимаете на клавишу Alt и, удерживая ее, набираете на цифровой клавиатуре цифры 0178 поочередно (то есть 0, затем 1, 7 и т.д.) или 0179 — в первом случае используется квадрат, а во втором — куб. После указании цифр снимаете палец с кнопки Alt.

Используйте левый Alt, если не сработал правый.

Если все сделано верно, вы увидите результат своих действий:

ВАЖНО! Проделывать указанные действия необходимо на англоязычной раскладке! Выберите ее при необходимости:

Есть несколько способов, как написать число-степень на клавиатуре

• Для написания квадратной степени: Alt+0178.
• Для написания кубической степени: Alt+0179.

Для работоспособности этого способа у вас на клавиатуре должна быть включена английская раскладка. Эта комбинация работает во всех редакторах, например блокноте, Word, NotePad, визуальном редакторе WordPress, практически везде, где можно набирать текст.

Второй способ — в редакторе Word

С помощью ворда можно ставить не только квадратную и кубическую степени, но и любые другие, в том числе буквенные. Например когда математические задачи требуют от степени числа быть переменной. Этот способ не связан с клавиатурой, больше с мышкой, но написать степень в Word очень просто. В верхнем меню есть специальный инструмент: надстрочный знак.

Выделяем число или буквы, которые нужно сделать степенью, и нажимаем на кнопку в верхнем меню, указанную на рисунке. Также можно воспользоваться сочетанием клавиш Ctrl+Shift+=. В результате можно получить любую степень, какая только нужна. Рядом есть инструмент «подстрочный знак», с помощью которого можно записывать число в нижнем регистре, например для логарифмов.

Третий способ — альтернативный для Word, работающий во всех версиях, в том числе старых

Нужно выделить текст, которой должен стать степенью, и нажать на него правой кнопкой. В появившемся меню нажать на вкладку «Шрифт».

В появившемся меню можно задать любые параметры выделенному тексту, в том числе и сделать его степенью. Для этого нужно поставить галочку в пункте «Надстрочный».

Вот и всё, теперь вы знаете, как написать степень на клавиатуре и можете применять этот навык в жизни.

Иногда во время работы с документами в Microsoft Word возникает необходимость написать число в степени, и в этой статье мы расскажем о том, как это делается.

Примеры решения задач

Пример

Задание. Вычислить:  $\frac{100^{3} \cdot 10^{8}}{2^{13} \cdot 5^{13}}$

Решение. Воспользуемся
свойствами степени

$$\frac{100^{3} \cdot 10^{8}}{2^{13} \cdot 5^{13}}=\frac{\left(10^{2}\right)^{3} \cdot 10^{8}}{(2 \cdot 5)^{13}}=\frac{10^{2 \cdot 3} \cdot 10^{8}}{10^{13}}=\frac{10^{6} \cdot 10^{8}}{10^{13}}=$$
$$=10^{6+8-13}=10^{1}=10$$

Ответ.  $\frac{100^{3} \cdot 10^{8}}{2^{13} \cdot 5^{13}} = 10$

Слишком сложно?

Что такое степень числа не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Представить в виде степени
$\left(y^{n+5}\right)^{2}:\left(\left(-y^{2}\right)^{3}\right)^{2}$ следующее выражение:

Решение. Решение. Используя
свойства степеней, получим:

$$\left(y^{n+5}\right)^{2}:\left(\left(-y^{2}\right)^{3}\right)^{2}=y^{2(n+5)}:\left(-y^{2 \cdot 3}\right)^{2}=$$
$$=y^{2 n+10}:\left(-y^{6}\right)^{2}=y^{2 n+10}: y^{6 \cdot 2}=$$
$$=y^{2 n+10}: y^{12}=y^{2 n+10-12}=y^{2 n-2}$$

Ответ.  $\left(y^{n+5}\right)^{2}:\left(\left(-y^{2}\right)^{3}\right)^{2}=y^{2 n-2}$